6. 理論
6.1. PDF解析
構造モデルから計算されるPDF解析に関わる関数を説明する。 ここでいう構造モデルとは、周期境界条件を仮定する原子配置データを意味する。
6.1.1. 部分二体分布関数 \(g_{\alpha\beta}(r)\)
下図に示されるように、ある原子を中心として他の原子が周りに存在する場合を考える。
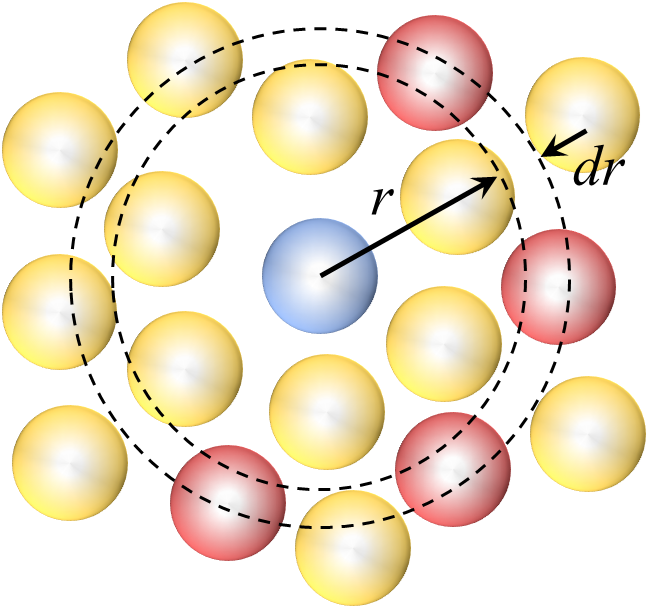
図 6.1 動径分布の概念図
1元系の構造モデルを仮定する場合、中心原子(青色)から半径 \(r\) と \(r+dr\) の微小半径で挟まれた領域に存在する原子(赤色) の数の期待値 \(dn(r)\) は二体分布関数 \(g(r)\) を用いて以下の式で表される。
上式を変形することによって、二体分布関数 \(g(r)\) は
と計算される。 ここで \(r\) は注目する原子からの距離、 \(N\) はセル内の原子数、 \(V\) はセルの体積である。
2元系以上の場合、元素のペアを考える必要がある。一方の原子を \(\alpha\) 、他方の原子を \(\beta\) とする場合、中心原子 \(\alpha\) および周辺原子 \(\beta\) の部分二体分布関数 \(g_{\alpha\beta}(r)\) は以下の式で計算される。
ただし、 \(N_{\alpha}\) は原子 \(\alpha\) の数、 \(dn(r)\) は中心原子 \(\alpha\) から半径 \(r\) と \(r+dr\) の微小半径で挟まれた領域に存在する原子 \(\beta\) の数の期待値である。
6.1.2. 二体分布関数 \(g(r)\)
二体分布関数 \(g(r)\) は、部分二体分布関数 \(g_{\alpha\beta}(r)\) を用いて以下のように計算される。
ここで \(c_{\alpha}\) は原子 \(\alpha\) の濃度( \(c_{\alpha}=N_{\alpha}/N\) )である。また、\(f_{\alpha}\) は原子 \(\alpha\) の散乱因子であり、X線回折の場合 \(Q\) に依存する値である。一方、中性子回折の場合に \(f_{\alpha}\) は散乱長であり、 \(Q\) に依存しない。これらの詳細を、下記の構造因子 \(S(Q)\) の節で述べる。また、分母は正規化項であり
と計算される。X線回折の場合、\(Q\) ごとに正規化項の計算が必要となる。
6.1.3. 部分構造因子 \(S_{\alpha\beta}(Q)\)
部分構造因子 \(S_{\alpha\beta}(Q)\) は、部分二体分布関数 \(g_{\alpha\beta}(r)\) の フーリエ変換で求めることができ、以下の式で計算される。
ただし、 \(\rho\) は原子の数密度( \(\rho=N/V\) )である。
6.1.4. 構造因子 \(S(Q)\)
構造因子 \(S(Q)\) は、部分構造因子 \(S_{\alpha\beta}(Q)\) を用いるFaber-Ziman型 [1] で計算される。
上式において、 \(f_{\alpha}\) や \(f_{\beta}\) として、X線回折の場合にX線散乱因子 (X-ray scattering factor)、 中性子回折の場合に中性子散乱長(Neutron scattering length)が用いられる。 X線散乱因子は、以下の近似計算が用いられることが多い。
ただし、上式における元素ごとの定数 \(a_i, b_i, c\) には文献 [2] の記載データ等が使われる。
また、中性子散乱長は、\(Q\) に依存しない値であり、元素ごとに定まる定数が用られる。中性子散乱長の具体的な値に関しては Wikipedia や NICTのDB を参照いただきたい。
6.1.5. 減衰二体分布関数 \(G(r)\)
減衰二体分布関数 \(G(r)\) (reduced PDF)は、二体分布関数 \(g(r)\) を用いて以下の式で計算される。
6.1.6. 全相関関数 \(T(r)\)
全相関関数 \(T(r)\) (total correlation function)は、二体分布関数 \(g(r)\) を用いて以下の式で計算される。
6.1.7. 動径分布関数 \(N(r)\)
動径分布関数 \(N(r)\) (Radial Distribution Function, RDF)は、全相関関数 \(T(r)\) を用いて以下の式で計算される。